Snake: Q Learning

Q-learning is a model free reinforcement learning algorithm. Being model-free, it figures out the transition probabilities of the Markov Decision Process (MDP) and the optimal policy without being explicitly told specifics of the environment its in through trial and error. I found this article contained a pretty clear analogy that explains the difference between model-based and model-free reinforcement learning.

The goal of the algorithm is to find an optimal policy in the sense of maximizing the expected value of the total reward over any and all successive steps, starting from the current state for any finite MDP.

Table Of Contents

Concepts

In order to discuss the algorithm, there are a few terms/concepts that should be explained:

1. State: A collection of variables and their specific values that describe a given situation.
2. Action: An action that can be taken to change states. Each state can have multiple valid actions.
3. Q: The value of taking an action in each state where the higher the value, the better the action is.
4. Policy: A list that tracks which actions are to be taken at any given state using the Q value.
5. Exploit: Choose the best action by its Q value.
6. Explore: Randomly choose an action rather than the best the best action. This is needed so that it does not get stuck doing the same actions it initially chose when there are more beneficial paths hidden behind what are initially considered bad moves.
7. Exploration Rate: A value between 0 and 1. This determines the probability agent will explore or exploit in this state. Starting off with a high rate that progressively decays allows agent to explore many options before refining its route.
8. Episode: An full iteration where the agent gets from start to any end point.
9. Step: Each step represents a single change in state.

The Bellman Equation

This is the equation that updates the value of Q on every iteration and makes Q-learning possible.

Where,

• s_t: State at time t.
• a_t: Action at time t.
• Q(s_t, a_t): Q value of a_t if taken in state s_t.
• max_aQ(s_t+1, a): The maximum Q value of all the actions that can be taken from state s_t+1.
• Reward: The value that is awarded when the agent enters a certain state.
• Temporal Difference Target (TDT): The new estimate of Q for the initial state after taking an action and taking into account its reward and actions available in the state it lands in.
• Discount factor: A value between 0 and 1. This affects how strongly the Q of actions that are available in the following state contribute to the TDT in the initial state.
• Temporal Difference: The difference in Q between the original estimate and the more accurate TDT.
• Learning Rate: A value between 0 and 1. This affects how strongly the temporal difference affects the initial value of Q.

The Algorithm

Here are the steps that my code follows in plain English:

1. Initialize the policy, this is typically done as a table where:
    * rows: states
    * columns: actions, cells: Q
    * Qs initialized to 0.
2. Until we reach the preset number of episodes,
    1. Set current actual state as state s,
    2. Until the agent gets a reward or dies, (or we hit a preset step limit)
        1. Decide whether to explore or exploit,
        2. Choose an action based on that decision,
        3. Use chosen action to advance the next state ns,
        4. Determine reward received for said action,
        5. Calculate new Q for s using the Bellman Equation,
        6. Update the old Q for s in the policy with the new Q.
        7. Set ns as s
    3. Decay exploration rate

Ultimately, what starts off as a table filled with 0s, will end up being an informative list telling the computer which actions are good or bad.

_{Image taken from Wikipedia}

The farther away the goal is from the agent, the more episodes and steps are required for the algorithm to work as intended. This is because the policy improves on itself by propagating the information about which action is a good choice from where the reward is. I've created a simple gif to show how the information propagates:

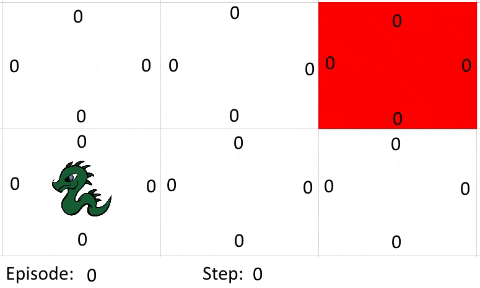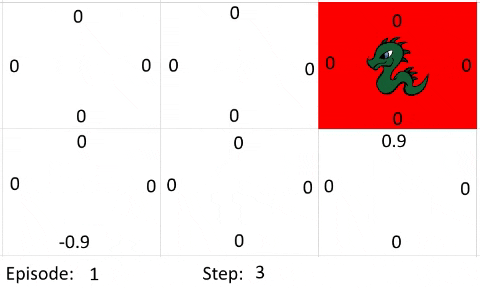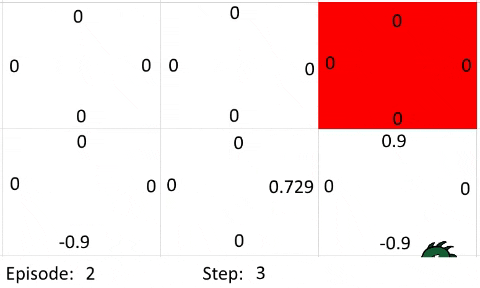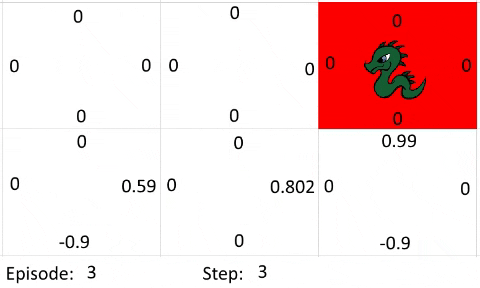
Let's just assume every step is an exploration move. The Bellman Equation used the following settings:

• Learning Rate: 0.9
• Discount Factor: 0.9
• Goal Reward: 1
• Out of Bounds Reward: -1

Implementation

In our case, each state is a location on the play area as that will determine the best action to take. The current state the snake is in will be based on where its head is located. Actions are to go North, South, East or West. Rewards are given only on eating an apple, or a negative reward (penalty) for intercepting itself or leaving the play area.

In my implementation, QLearn is an object that is initialized with all the settings needed for the algorithm:

const QLearn = (nEpisodes, maxSteps, exploreRate, exploreDecay, exploreMin, 
  learnRate, discountRate, eatReward, deathReward, cumulativePolicy=true) => {
  
  const ql = {}
  ql.nEpisodes = nEpisodes
  ql.maxSteps = maxSteps
  ql.exploreRate = exploreRate
  ql.exploreDecay = exploreDecay
  ql.exploreMin = exploreMin
  ql.learnRate = learnRate
  ql.discountRate = discountRate
  ql.eatReward = eatReward
  ql.deathReward = deathReward
  ql.cumulativePolicy = cumulativePolicy

  ql.actionMap = new Map()
  game.DIRECTIONS.forEach((d, i) => { ql.actionMap.set(i, d) })
  game.DIRECTIONS.forEach((d, i) => { ql.actionMap.set(d, i) })

  ql.policy = null

Here if cumulativePolicy is false, the policy will reinitialize on every call of update() which we'll talk about later. nEpisodes and nSteps must also be increased significantly, otherwise the snake may not be able to find the apple during the update and end up just infinitely running in circles.

actionMap lets us look up the index of actions in the Q table or use the index to look up the actions.

The very first method that is needed is for initializing a blank policy. This just takes the number of cells in to x and y axis of the play area (because each state is only defined by the location of the head), and makes a 3D matrix where the final dimension is an array of Q values where each index represents a separate action defined in actionMap.

ql.initPolicy = (nx, ny) => {
  const mkQs = () => Array(game.DIRECTIONS.length).fill(0)
  return Array.from(Array(nx), _ => Array.from(Array(ny), _ => mkQs()))
}

Skipping all the helper methods, we can go straight into the update() method. To use it, we must pass the next() function and state object that are currently in use in the game to run accurate simulations in each episode.

ql.update = (next, state) => {
  let exploreRate = ql.exploreRate
  // If no policy is given, start fresh
  if (ql.policy==null || state.justEaten || !ql.cumulativePolicy) ql.policy = ql.initPolicy(state.nx, state.ny)
  // Play the game nEpisodes times from the current start to gather information
  for(let ep=0; ep<ql.nEpisodes; ep++) {
    let s = state;
    // Each episode is limited to a maximum number of steps that can be taken
    for(let step=0; step<maxSteps; step++) {
      const head = s.snake[0]
      // Get an action to try out
      const ai = ql.isExplore(head, exploreRate) ? ql.getRandomActionIndex() : ql.getActionIndex(head)
      const ns = next(s, {direction: ql.actionMap.get(ai)})
      // Get reward based on outcome of the action
      const r = !ns.isAlive ? ql.deathReward : (ns.justEaten ? ql.eatReward : 0)
      // Calculate and update the Q for the current head location
      const nQ = ql.calcQ(ql.getQ(ai, head), r, ql.maxQ(ns.snake[0]))
      ql.setQ(ai, nQ, head)
      // If the snake is dead or just ate, end the episode early, otherwise advance state
      if(!ns.isAlive || ns.justEaten) break
      else s = ns
    }
    // Exploration rate decays linearly with each episode until a minimum is reached
    exploreRate = Math.max(ql.exploreMin, exploreRate - ql.exploreDecay)
  }
}

This method basically just follows the algorithm set out in the earlier section. Just some notes:

• At the start of every call, the exploration rate is saved to a local variable to prevent mutating the stored value in the object.
• The policy reinitializes itself when the snake had just eaten because the apple would have moved, making it pointless to keep the old policy.