Sudoku: DLX (Dancing Links)

Link to project here.

In computer science, dancing links is a technique for reverting the operation of deleting a node from a circular doubly linked list. This technique was popularized by Donald Knuth in his paper about it in from 2000.

This particular part of the project will focus much less on keeping with the functional programming style as making the Dancing Links data structure work with the rules of the style would be quite time consuming.

Exact Cover Matrix Using Doubly Linked Lists
The DLX Algorithm
- The Usual Way
- The Non-Recursive Way
Conclusion

Exact Cover Matrix Using Doubly Linked Lists

In an exact cover problem, the exact cover matrix (ECM) is generally a very sparse matrix. Just have a look at the first five rows for a 4x4 Sudoku puzzle.

1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0
1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0
0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0

For 9x9 Sudoku, its ECM has 236196 cells, but only 2916 are actually occupied, making traversal extremely inefficient. However, if we represented this matrix as a doubly linked list instead, we'd be able to instantaneously hop between cells that are occupied. This also has the added bonus of allowing us to easily remove rows and columns, and then reinsert them using the method that was described before.

For my implementation, which I shall just call a DLM (Dancing Links Matrix), there are 3 objects used to create this representation:

Node x, which represents the 1s in the matrix. These objects are linked together as vertical and horizontal doubly linked lists using the following properties:
- x.left : points to the node on its left, used to link nodes together in a row.
- x.right : points to the node on its right, used to link nodes together in a row.
- x.up : points to the node above it, used to link nodes together in a column.
- x.down : points to the node below it, used to link nodes together in a column.
- x.column : points to the header of the column it is a member of.
- x.name: the row index of the cell it represents in the ECM.
Column y, which functions as the header for each column of nodes. It has the same properties of a node with some one addition:
- y.left : points to the column on its left, used to link columns together in a row (header row).
- y.right : points to the columns on its right, used to link columns together in a row.
- y.up : points to the node at the "bottom" of the column.
- y.down : points to the node at the "top" of the column.
- y.column : unused.
- y.size : refers to the number of nodes in the column.
- y.name : the index of the column it represents in the ECM.
Root h, its sole purpose is to be the point of entry for the DLM, thus there are no nodes connected to it. Its only 2 properties are:
- h.left : points to the column at the "end" of the header row.
- h.right : points to the column at the "start" of the header row.

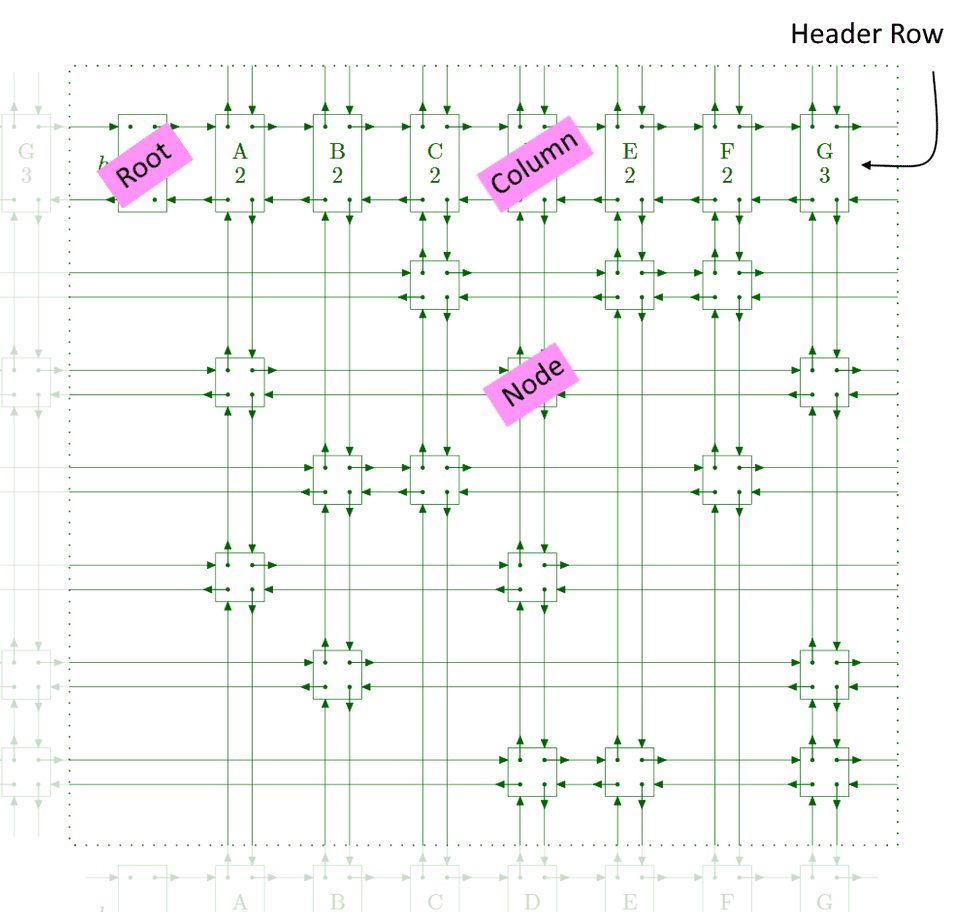
Here's a visualization of how they fit together, original was lifted from the paper:

Node Methods

The methods in these nodes are only used when creating the DLM from scratch. insertRight() inserts a node n to the right of itself, and insertDown() inserts a node n below itself. Because all nodes start out pointing to themselves in all directions, the insertion methods will always result in a circular linked list.

node.insertRight = n => {
  // Update pointers in n
  n.left = node
  n.right = node.right
  // Update pointers in new n.right, originally points to node, now n
  n.right.left = n
  // Update pointers in node
  node.right = n
}

Column Methods

The paper emphasizes two key operations at the very start, insertion and removal of a node.

Say we have a node x we want to remove from our DLM. To remove x from the list, we simply have to do the following:

x.left.right = x.right
x.right.left = x.left

And then to reinsert x into the list:

x.left.right = x
x.right.left = x

The key here is that because x still points toward its original left and right neighbors even after being removed from the list, undoing the removal is very straight forward. Thus, when traversing a complex data structure involving a large number of interacting doubly linked lists, this simple idea makes it possible for the program to easily run in reverse (backtracking) until it wants to move forward again. This is the basis for the cover() and uncover() methods of the column objects.

The cover() method removes the column from our DLM, as well as all rows that have a node in the column. It goes from top to bottom, moving to the right.

column.cover = () => {
  // Point column header's left right neighbors at each other
  column.right.left = column.left
  column.left.right = column.right
  // Going top to bottom, i being a row in the column
  let i = column.down
  while (i != column) {
    // Left to right, j being a node in row i
    let j = i.right
    while (j != i) {
      // Point j's up down neighbors at each other
      j.down.up = j.up
      j.up.down = j.down
      // Because j has been covered, update the size of the column it belongs to
      j.column.size--
      // Continue to the right
      j = j.right
    }
    // Continue to the bottom
    i = i.down
  }
}

The uncover() method reinserts the column, as well as all rows that have node in the column. This goes from bottom to top, moving to the left. The paper points out that it is important to reinsert rows (i) in reverse order of them being removed, this need not be adhered to when reinserting the individual nodes (j).

column.uncover = () => {
  // Going bottom to top, i being a row in the column
  let i = column.up
  while (i != column) {
    // Right to left, j being columns that row i satisfies
    let j = i.left
    while (j != i) {
      // Because j has been uncovered, update the size of the column it belongs to
      j.column.size++
      // Point j's up down neighbors to j again
      j.down.up = j
      j.up.down = j
      // Continue to the left
      j = j.left
    }
    // Continue to the top
    i = i.up
  }
  // Point column header's left right neighbors at column again
  column.right.left = column
  column.left.right = column
}

Generating the Dancing Links Matrix from an Exact Cover Matrix

Because I already have a function to create an ECM, the focus will be on importing it into this data structure. The first thing we need to do is create the header row, which contains a column object for every column in the ECM.

const columns = []
for (let i=0; i<ecMatrix.get(0).count(); i++) {
  columns.push(dancingLinks.Column(i))
  // Insert new columns to the right of their predecessors
  if (i>0) columns[i-1].insertRight(columns[i])
}

The columns are named after the column index they represent, so that they can be easily identified for representing the solution on the Sudoku grid. They are added to an array to make them directly accessible when generating the rows.

We start the next step in the process by iterating through each cell in the ECM. When we come across a non-empty cell, we can look up the column object for the column index we are in using the columns array, and the create a node linking to the column. As we progress through the row, nodes are continuously joined vertically to their respective column and horizontally the node that came before it. Nodes are named after the row index they represent in the ECM.

// For each row in the ecMatrix,
for (let i=0; i<ecMatrix.count(); i++) {
  let prevNode = null
  // And each column in the ecMatrix,
  for (let j=0; j<ecMatrix.get(0).count(); j++) {
    // If row i satisfies column j, create a node here
    if (ecMatrix.getIn([i,j])>0) {
      const c = columns[j]
      const node = dancingLinks.Node(c, i)
      // Because iteration is going top to bottom, insertion will always
      // be at the bottom of the column (which is always above the header)
      // Vertical Link
      c.up.insertDown(node)
      c.size++
      // Because iteration is going left to right, insertion will always
      // to the right of the previous node
      // Horizontal Link
      if (prevNode!=null) prevNode.insertRight(node)
      prevNode = node
    }
  }
}

Finally once we have gone through the whole ECM, we just insert the root object after the last column. This is just a column object that does not have any rows connected to it. As said early, this functions as an entry point for the DLM.

// Insert root object
const root = dancingLinks.Column()
columns[columns.length-1].insertRight(root)
return root

Initializing the DLM

If we run the algorithm from a fresh DLM for a very, very long time, we'd be able to find every possible solution for every Sudoku puzzle. However, this might not be very helpful in solving specific puzzles. Thus, we need to prep the DLM before use.

This is done by iterating through every cell in the initial Sudoku grid. If there is a value there, find the corresponding row in the ECM and then covering every column that it satisfies in the DLM.

const init = (grid, ecMatrix, root) => {
  const matrix = grid.get("matrix")
  // Check every cell in the grid
  for (let i=0; i<matrix.count(); i++) {
    for (let j=0; j<matrix.count(); j++) {
      const v = matrix.getIn([i,j])
      // If it already has a value, cover the columns it satisfies
      if (v != " ") { 
        const rowInd = exactCover.getRowIndex(i, j, v, grid)
        // Get the columns that row satisfies
        const columns = ecMatrix.get(rowInd)
          .map((v, i) => v>0? i : -1)
          .filter(v => v>=0)
          .toSet()
        // Find the column object in dlx and cover
        for (let c=root.right; c!=root; c=c.right) { 
          if (columns.has(c.name)) c.cover() 
        }
      }
    }
  }
}

In my particular implementation, this step is embedded in the mkState() function that is similar to what we've seen before.

const mkState = grid => {
  // Cover columns that have already been satisfied by the initial grid
  const init = (grid, ecMatrix, root) => {
    ...
  }

  const state = {}
  state.ecMatrix = exactCover.mkMatrix(grid)
  state.lookup = exactCover.mkLookup(grid)
  state.root = dancingLinks.importECMatrix(state.ecMatrix)
  init(grid, state.ecMatrix, state.root)
  state.level = 0
  state.stack = [{c:null, r:null}]
  state.solution = []
  state.solutions = []
  
  return state
}

The solution array is for tracking the current solution being worked on, while the solutions array stores all solutions that have been found so far. The level and stack variables will be explained later.

The DLX Algorithm

With the data structure implemented, the algorithm is basically Algorithm X, just a depth first search through the DLM, finding row combinations that result in an empty DLM:

Check if there are columns remaining in DLM A, if there aren't then the current solution is valid, exit.
Otherwise choose a column c to satisfy.
Cover c.
Choose a row r that satisfies c.
Add r to the partial solution.
For each column j that r also satisfies,
  Cover j.
Repeat this algorithm recursively on the reduced A.
Remove r to the partial solution.
For each column j that r also satisfies,
  Uncover j.
Uncover c.

The Usual Way

Following the algorithm, we start off by checking if there is a solution.

const search = (state, limit=0, isGreedy=true) => {
  const root = state.root
  const solution = state.solution
  const solutions = state.solutions
  const _search = k => {
    if (root.right == root) solutions.push(solution.concat())

If there is no solution, then select a column, either the first one on the list, or the smallest one (S heuristic), the latter being the more efficient choice. It is basically the same reasoning behind the Greedy variants of the other algorithms in this project, and the paper provides numbers and graphs to back it up.

let c = null
if (isGreedy) {
  // S heuristic
  for (let j=root.right; j!=root; j=j.right) {
    if (c==null || j.size < c.size) c = j
  }
} else {
  c = root.right
}

Once a column is chosen, it is then removed using cover() so that it is removed from all future consideration along this path. We then consider each row in the column, covering all columns that the row satisfies.

We then recur deeper with _search() until we find a solution or we hit a dead end (column with no rows).

After which we backtrack and uncover() the current row, and move on the the one below it. When the entire column has been searched, we must uncover() the column we are on before backtracking naturally occurs again by reaching the end of the function.

c.cover()
// Then go through rows of column depth first
for(let r=c.down; r!=c; r=r.down) {
  // Choose a row then cover all columns that it satisfies
  solution.push(r)
  for(let j = r.right; j!=r; j=j.right) {
    j.column.cover()
  }
  // Search assuming this row is part of the solution
  _search(k+1)
  // Undo this row and move on to the next
  r = solution.pop()
  c = r.column
  for(let j = r.left; j!=r; j=j.left) {
    j.column.uncover()
  }
  // This is to limit the number of solutions found and exit early
  if (limit>0 && solutions.length >= limit) break
}
// If all rows have been searched, uncover this column
c.uncover()

That is the whole algorithm. It will only end once it has gone through every possible combination of moves it can reach and found every solution. That's why I added line 18 which allows us to exit early.

The Non-Recursive Way

While it works great out of the box, I still need break it into discrete steps like I did with the other algorithms in order to be able to visualize its progression. I was having a lot of trouble figuring it out until this implementation by Antti Ajanki and Tom Boothby showed me the light.

In the previous algorithms, I was basically storing the entire state of the algorithm after each move in a stack and then just recalling it as needed. This same approach would not work due to the mutations that need to happen to make progress.

The trick is in fact, to use a stack to simulate recursion by storing the state at each level of "recursion" in said stack. By keeping track of which level we are in the "recursion", we can immediately pick up where we left off while being able to backtrack easily. This also has the added bonus of being able to stick closely to the original algorithm, just with more housekeeping.

Just so we are clear, the main additions are the state.stack and state.level.

At the start of each step, we load the state of the algorithm at the current level. Where c is the currently selected column, and r is the current node in the column.

let {c, r} = state.stack[state.level]

If this level was just created via "recursion", c will be null. Similar to the original, we first check if there is a solution. If there is, store it and then backtrack by subtracting a level. If there is no solution, we select a column just like we did before and then cover it.

if (c==null) {
  if (state.root.right==state.root) {
    // Check if its complete
    // Store the solution
    state.solutions.push(state.solution.concat())
    // Backtrack
    state.level--
    return data
  } else {
    // Otherwise Choose a column to satisfy
    if (isGreedy) {
      // S heuristic
      for (let j=state.root.right; j!=state.root; j=j.right) {
        if (c==null || j.size < c.size) c = j
      }
    } else {
      c = state.root.right
    }
    // Cover the chosen column and iterate through the rows
    c.cover()
    state.stack[state.level] = {c:c, r:c}
    r = c
  }
}

Moving on, if r is not currently equal to c that must mean that we already processed it in the previous call. So we must undo r before proceeding further.

if (c != r) {
  state.solution.pop()
  for(let j = r.left; j!=r; j=j.left) {
    j.column.uncover()
  }
}

If the node below it is not a column, then we can set that as the current r and then continue the "recursion" by storing the current c and r in the stack, and then increasing the level and initializing the next level of "recursion". We will then end up there on the next call.

if (r.down != c) {
  // add r.down to the solution
  r = r.down
  state.solution.push(r)
  for(let j = r.right; j!=r; j=j.right) {
    j.column.cover()
  }
  // Record the state of the current level
  state.stack[state.level] = {c:c, r:r}
  // and go deeper into the stack
  state.level++
  // Make sure the next level in the stack is clear
  // Grow stack if needed
  if(state.stack.length==state.level) {
    state.stack.push({c:null, r:null})
  } else {
    state.stack[state.level] = {c:null, r:null}
  }
}

If we have reached the end of the column c or if there were no rows to begin with, then we simply uncover() and backtrack.

else {
  c.uncover()
  state.level--
}

This step function can be continuously called until it has found every solution. For the app itself, I just limited it to only a single solution.

Conclusion

This algorithm turned out to be quite elegant with the addition of the Dancing Links data structure. Each step is also extremely efficient and fast, probably even more so than it's more simplistic competitor, the Greedy Depth First Search. It hasn't even broken a sweat with all the puzzles I've thrown at it. It'd be interesting to see how the algorithms compare with each other if I ever get around to benchmarking them.